Trees and Graphs
DISCLAIMER: If you don’t know what a tree is, don’t read the rest of this page.
A Binary Tree is a Tree, but a Tree is not a Binary Tree - Barack Obama
Trees
Binary Tree
- Each node has at most 2 children
Binary Search Tree
- It is a binary tree but follows a simple rule
- :large_blue_diamond: all left descendants <= the node < all right descendants :large_orange_diamond:
- The equality can appear on the left or right side, depends on the situation
Complete Binary Tree
- A Binary Tree in which every level is fully filled, except for the last level
- The last level is filled from left to right
Full Binary Tree
- A Binary Tree in which every node has either 0 or 2 child nodes
- :exclamation: None of the node has 1 child
Perfect Binary Tree
- A Binary Tree
- which is Complete and Full
:star: It has 2k - 1 nodes, where k = number of levels in the tree
Binary Heaps
Advantages of Heap over Array
- O(logn) to insert in heap, but O(n) to insert in sorted array
- O(logn) to extract min / max from heap, but O(n) in array
- O(1) to find min / max from heap, but O(n) in array
Min-heap
- A min-heap is a complete binary tree, where each node is smaller than its children
- The root is the minimum element in the tree
- There are 2 key operations on min-heap
insertandextract_min - Min Heap Implementation
insert
- Insert the new element at the bottomost rightmost spot (as to maintain the complete binary tree property)
- Fix the tree by swapping the new value with its parent till an appropriate spot is found
- Time Complexity - O(logn)
extract_min
- Replace the minimum element at the top with the bottommost rightmost element
- Fix the tree by swapping this value with one of the children till the min-heap property is restored
- Time Complexity - O(logn)
Max-heap
- A max-heap is a complete binary tree, where each node is larger than its children
- The root is the maximum element in the tree
- There are 2 key operations on max-heap
insertandextract_max - Max Heap Implementation
insert
- Insert the new element at the bottomost rightmost spot (as to maintain the complete binary tree property)
- Fix the tree by swapping the new value with its parent till an appropriate spot is found
- Time Complexity - O(logn)
extract_max
- Replace the maximum element at the top with the bottommost rightmost element
- Fix the tree by swapping this value with one of the children till the max-heap property is restored
- Time Complexity - O(logn)
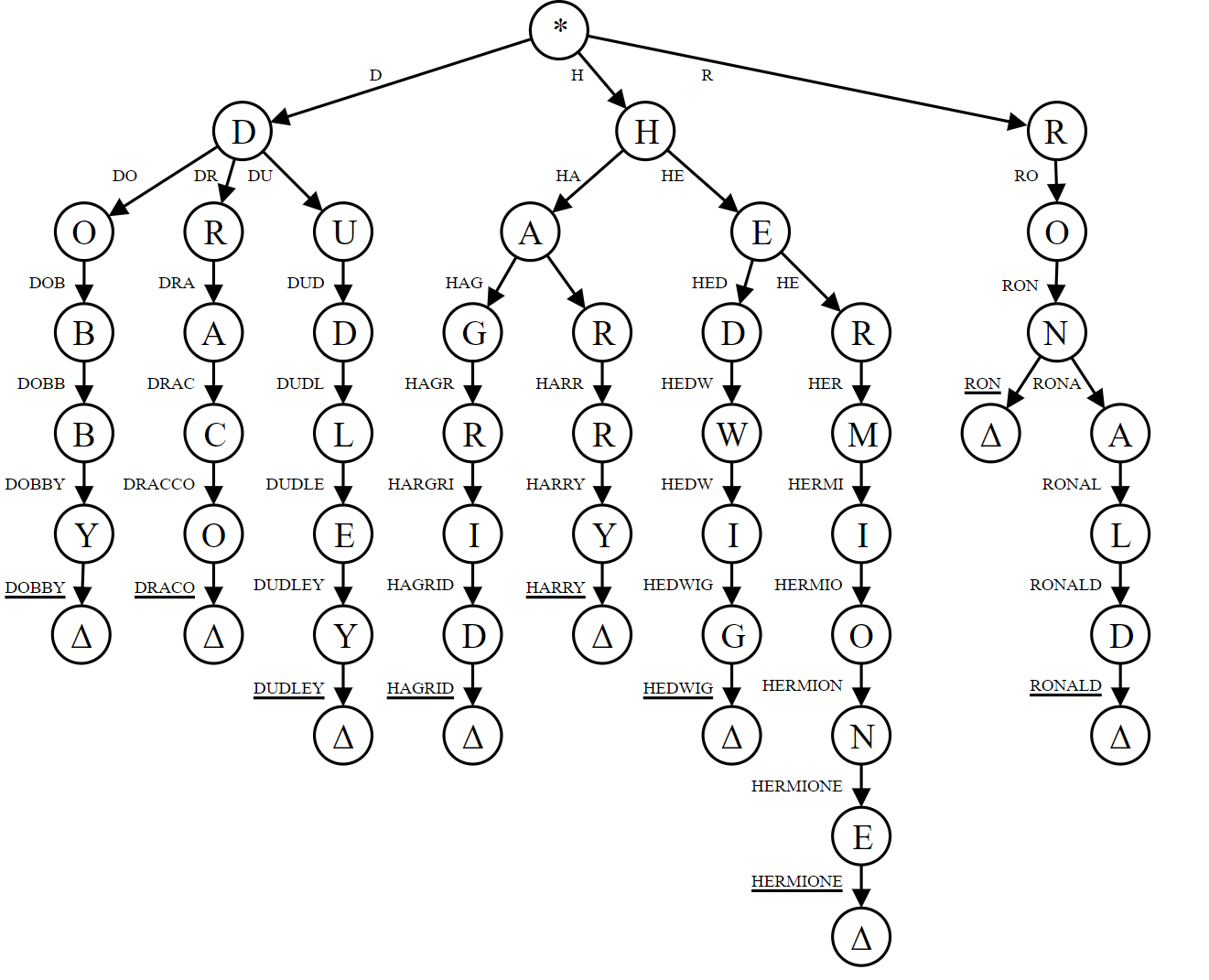
Tries
What is a Trie ?
- aka Prefix Tree
- It is a type of a search tree
- A trie is an n-ary tree in which characters are stored at each node
- Words can be re trie ved by traversing down a branch
Structure
-
Each trie has an empty root node, with links to other nodes - one for each possible alphabetic value
-
Each node contains an array of pointers to child nodes - one for each possible alphabetic value
-
:exclamation:NOTE - The size of the trie is directly correlated to the size of the alphabet being represented by the data structure
-
Every node in trie (including the root node) at least has these 2 aspects
- A value, which might be NULL
- An array of reference to child nodes which also might be NULL
Introduction to Fenwick and Segment Trees
- Consider an
arr[0 ... n-1] - We want to do 2 operations on this array
- Compute the sum of first i elements
- Modify the value of a specified element
arr[i] = xwhere0 <= i <= n-1
- Simple solution is to run a loop for calculating sum
O(n)and modify value by simple indexing, soO(1) - What if we want to perform both operations in
O(logn) - Recommended reading: Efficient Bit Operations
- Continue reading
Segment Tree
Representation
- It is represented as an array
- Left subtree is stored at
2*idx + 1 - Right subtree is stored at
2*idx + 2
Construction
- It has 3 methods,
build(),update(),query()
Time Complexity
build():O(n)update():O(logn)query():O(logn)
Applications
- To get range sum of an array in
O(logn)time. - Range sum, Range minimum/maximum, Range GCD, etc.
- You have an array.
- You want to perform frequent range queries and updates.
Fenwick Tree / Binary Indexed Tree
Representation
- It is represented as an array
- Let the array be
BITree[] - The size of the Binary Indexed tree is equal to the size of input array
Construction
- Initialize the
BITree[]as 0 - Then we call
update()for all the indexes
Operations
There are 2 operations
getSum(x)- Returns the sum of the subarrayarr[0 ... x]- Initialize the output
sumas0, the current index asx + 1 - Do following while the current index is greater than
0- Add
BITree[index]tosum - Go to the parent of
index- How to go to the parent ? By removing the right most set bit
index=index - (index & (-index))
- Add
- Return
sum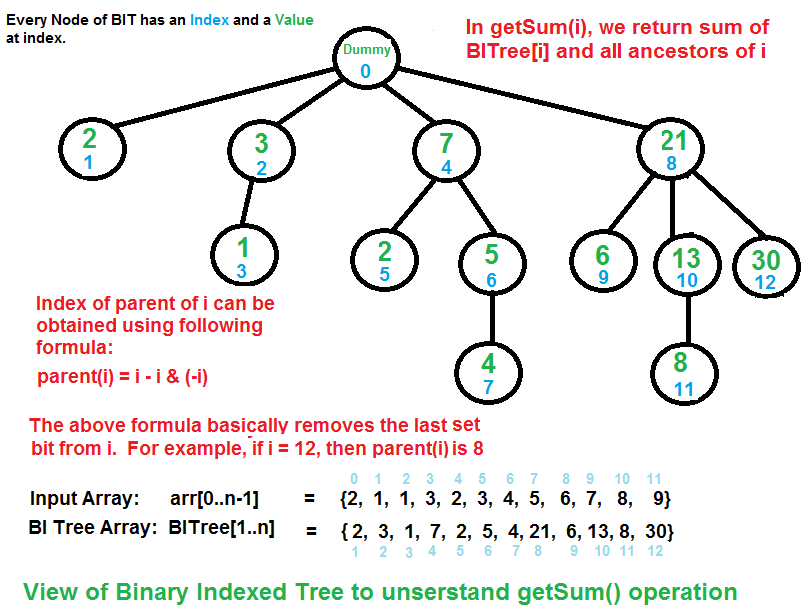
- Initialize the output
update(x, val)- Update the Binary Indexed Tree by performingarr[index] += val, it will make changes toBITree[]- Initialize current index as
x + 1 - Do the following while the current index is smaller than or equal to
n- Add the
valtoBITree[index] - Go to the next element of
BITree[index]- The next element can be obtained by incrementing the last set bit of the current index
index = index + (index & (-index))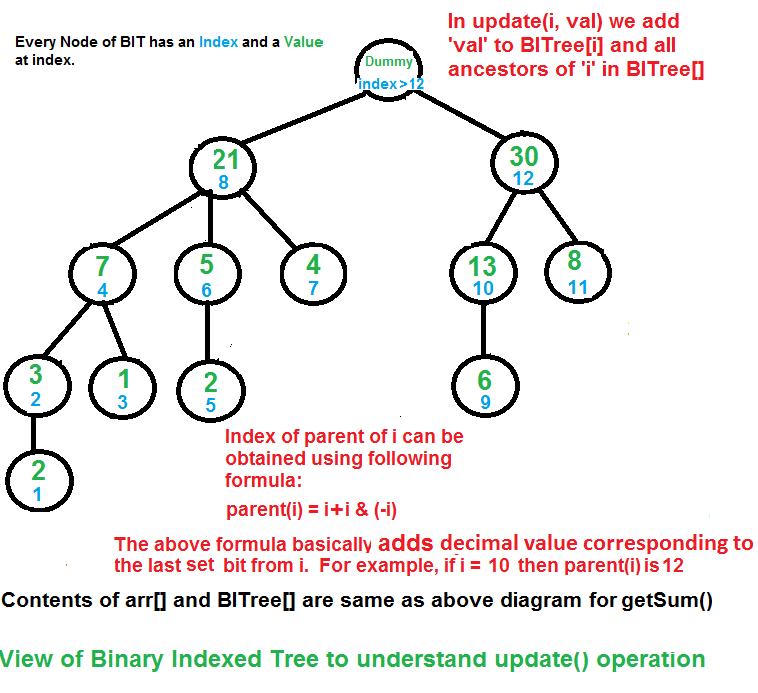
- Add the
- Initialize current index as
Applications
- To get prefix sum of an array in
O(logn)time - To update the prefix sum array in
O(logn)time
A tree is actually a type of graph, but not all graphs are trees - Doge
Graphs
- A tree is a connected graph without cycles.
- A graph is a collection of nodes with edges between them
Theory
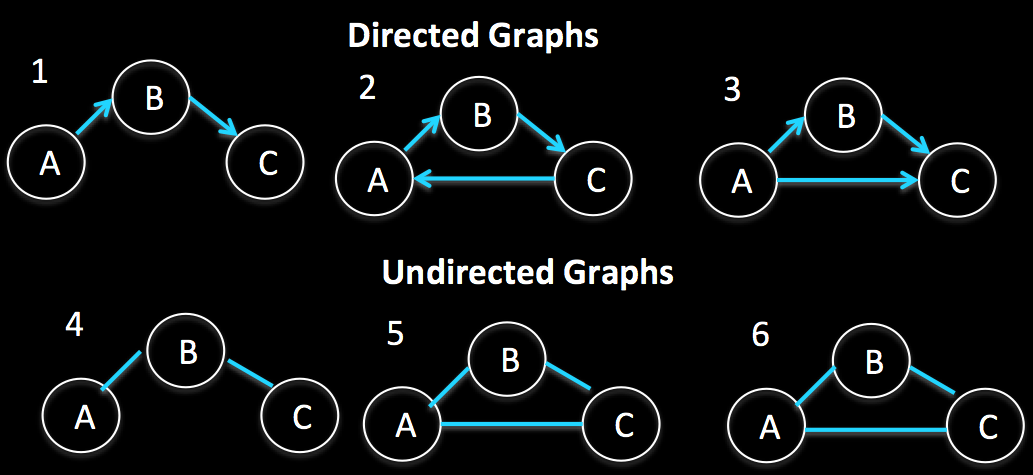
Directed and Undirected
- Directed edge, one way
- Undirected edge, two way
Weighted
- Every edge has a weight assigned to it
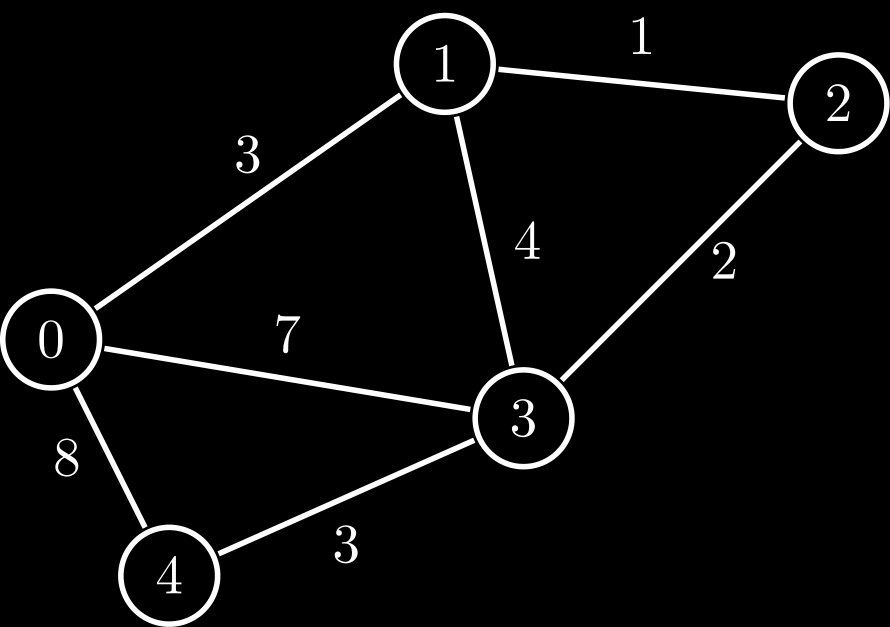
Rooted Tree
- It is a tree with a designated root node
- Every edge either points away from or towards the root node
- When edges point away from the root -> arborescence (out-tree)
- When edges point away from the root -> anti-arborescence (in-tree)
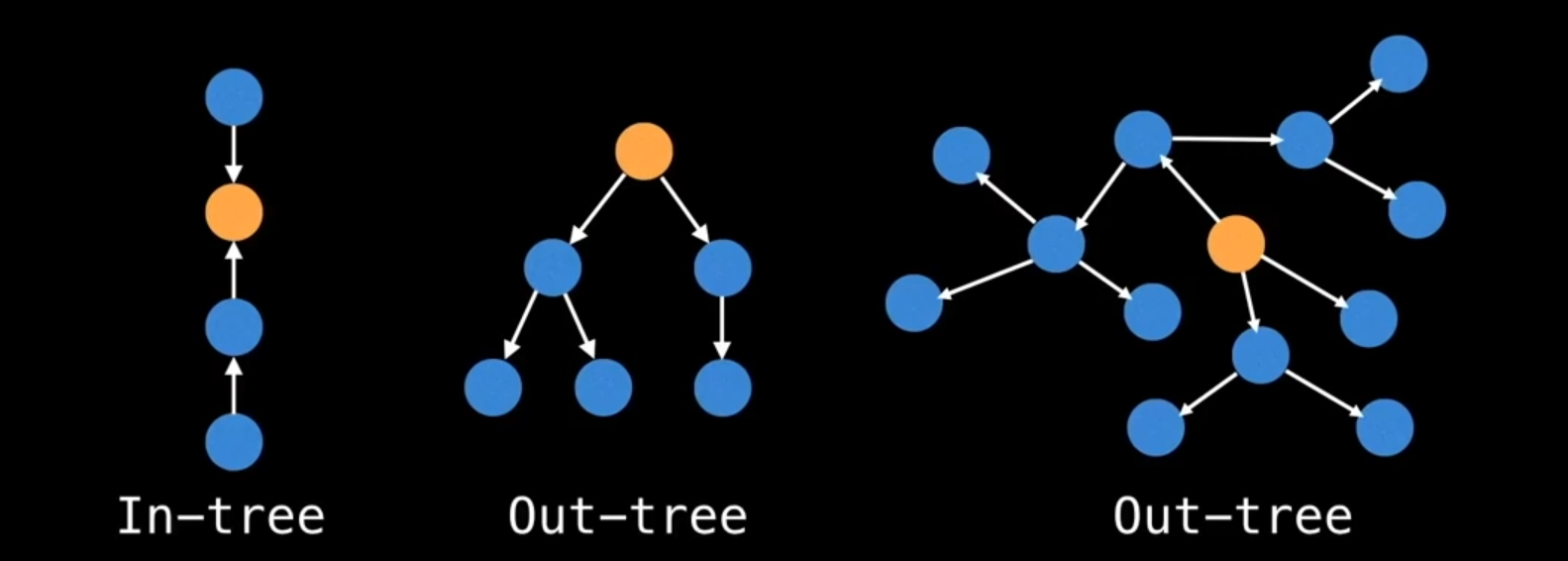
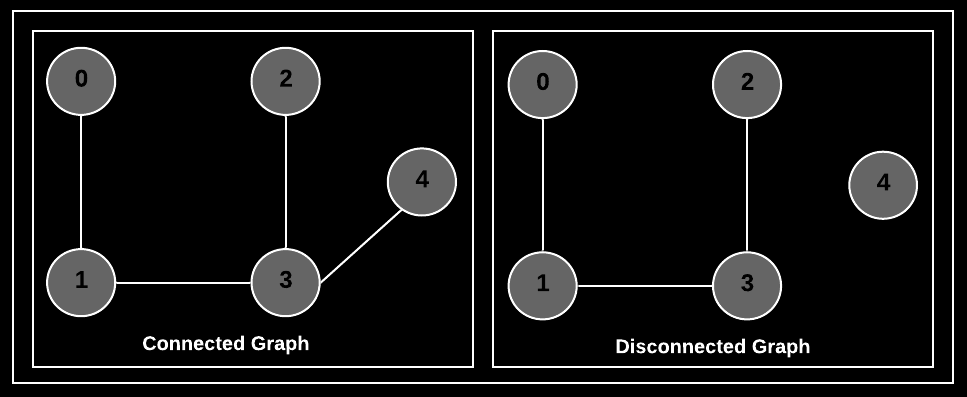
Connected and Disconnected
- If there is a path from any point to any other point in the graph, it is called a connected graph
- If there exists multiple disconnected vertices and edges, then it is called a disconnected graph
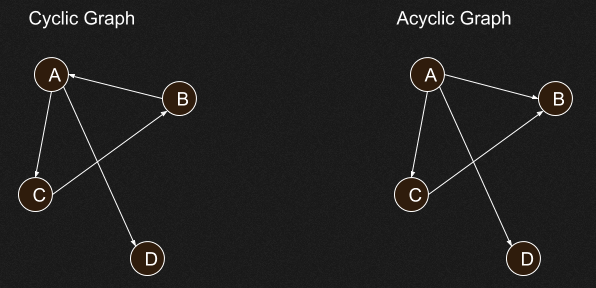
Cyclic and Acyclic
- If a graph contains cycles, then it is called a cyclic graph
- A graph containing 0 cycles is an acyclic graph
Directed Acyclic Graph (DAGs)
- Directed graphs with no cycles
- These graphs play an important role in representing structures with dependencies
Bipartite Graph
- A bipartite graph is one whose vertices can be split into two independent groups U, V such that every edge connects between U and V
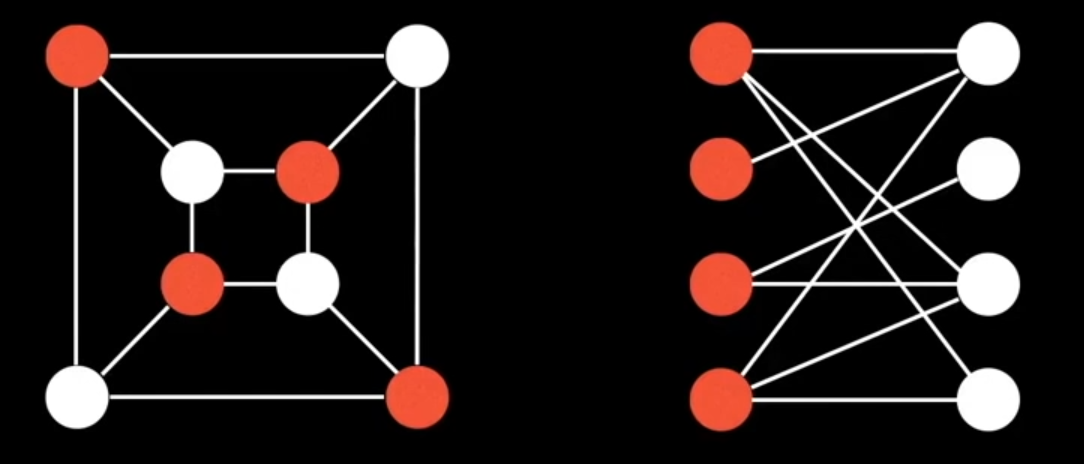
Strongly Connected Components
- SCCs can be thought of as self-contained cycles within a directed graph where every vertex in a given cycle can reach every other vertex in the same cycle
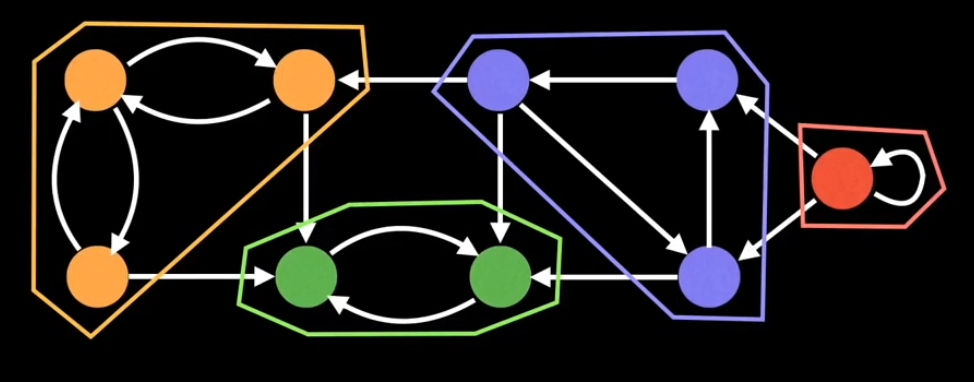
Algorithms
Depth-first Search
What can DFS do?
- Compute a graph’s minimum spanning tree
- Detect and find cycles in a graph
- Check if a graph is bipartite
- Find strongly connected components
- Topologically sort the nodes of a graph
- Find bridges and articulation points
- Find augmenting paths in a flow network
- Generate mazes
Time Complexity
O(V + E)
Breadth-first Search
What can BFS do?
- Find shortest path on unweighted graph
- Number of Islands in a grid, quite popular problem
Time Complexity
O(V + E)
Topological Sort
- It is only for Directed Acyclic Graphs (DAG)
- It is a linear ordering of vertices such that for every directed edge (u,v) , vertex u comes before v in the ordering
- Time Complexity =
O(V + E)
Applications
- School class prerequisites
- Program dependencies
- Event Scheduling
- Assembly Instructions
Single-Source Shortest Path in a DAG
- Popular application of Topological Sort
- Find the shortest path from one given source node to every other node in the graph
- Only valid for DAGs though
Dijkstra’s Algorithm
Algorithm
- Maintain a ‘dist’ array where the distance to every node is +ve infinity. Mark the distance to the start node ‘s’ to be 0.
- Maintain a PQ of key-value pairs of (node_index, distance) pairs which tell you which node to visit next based on sorted min value.
- Insert (s,0) into the PQ and loop while PQ is not empty pulling out the next most promising (node_index, distance) pair.
- Iterate over all edges outwards from the current node and relax each edge appending a new (node_index, distance) key-value pair to the PQ for every relaxation.
- SSSP Algorithm for graphs with non-negative edge weights
- Time Complexity =
O(E * log(V)) - :warning: NOTE: One constraint for Dijkstra’s algorithm is that the graph must contain non-negative edge weights.
- This constraint is imposed to ensure that once a node has been visited its optimal distance cannot be improved
- This property enables Dijkstra’s algorithm to act in a greedy manner by always selecting the next most promising node
Bellman-Ford Algorithm
Algorithm
- v = number of nodes in the graph
- e = number of edges in the graph
- s = starting node
- dist[] = distance to each node from ‘s’
- Maintain a ‘dist’ array of size v, initially the distance to each node is +ve infinity
- Set the distance to starting node as 0
- Relax each edge v-1 times
- Why v-1 times? Because we don’t know the sequence in which the edges will be processed, since the longest path can be v-1 nodes long, to consider all the edges we run it v-1 times.
- For more clarification Why do we need to relax all the edges v-1 times in Bellman-Ford?
- SSSP algorithm that can detect negative cycles
- Time Complexity -
O(EV) - When to use? When the graph has negative cycles because Dijkstra’s can’t handle negative edge weights
Floyd-Warshall Algorithm
Algorithm
- The Memo Table: it will be 3-D matrix
dp[k][i][j] - which stores shortest path from
itojrouting through0toknodes - specifically,
dp[n-1]is the 2-D matrix solution we are looking for - when
k = 0,dp[0][i][j] = adj[i][j] - otherwise,
dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k] + dp[k-1][k][j]) - we can convert memo table to 2-D, by changing the values in place, rather than storing the state
k-1 - so it reduces to, when
k = 0,dp[i][j] = adj[i][j] - otherwise,
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j])
- This is an all-pairs shortest path algorithm.
- It finds the shortest distance between all pairs of nodes
- Time Complexity -
O(V^3) - ideal for graphs no larger than a couple of hundred nodes
- it can detect negative cycles
Bridges and Articulation Points
Bridge
A bridge/cut edge is any edge in a graph whose removal increases the number of connected components
Articulation point
An articulation point/cut vertex is any node in a graph whose removal increases the number of connected components
flowchart LR
node0((0))
node1((1))
node2((2))
node3((3))
node4((4))
node5((5))
node6((6))
node7((7))
node8((8))
node0 --- node1
node0 --- node2
node1 --- node2
node2 --- node3
node3 --- node4
node2 --- node5
node5 --- node6
node5 --- node8
node6 --- node7
node7 --- node8
In the above graph Bridges - {2,3}, {3,4}, {2,5} and Articulation points - {2}, {5}, {3}
Significance of bridges and articulation points
Bridges and articulation points are important because they often hint at weak points, bottlenecks or vulnerabilities in a graph. Therefore it is important to be able to quickly find/detect when and where these occur.
Low-link value
The low-link value of a node is the smallest (lowest) id reachable from that node when doing a DFS (including itself)
Tarjans Algorithm for finding bridges
Code - Find Bridges
Eulerian Path and Circuit
Eulerian Path
An Eulerian Path is a path of edges that visits all the edges in a graph exactly once.
Eulerian Circuit
An Eulerian Circuit is an Eulerian Path which starts and ends on the same vertex.
What condition are required for a valid Eulerian Path/Circuit?
Depends on the kind of graph:
Undirected Graph
Eulerian Circuit
- Every vertex has an even degree
Eulerian Path
- Either every vertex has even degree
- Or exactly 2 vertices have odd degrees
Directed Graph
Eulerian Circuit
- Every vertex has equal indegree and outdegree
Eulerian Path
- At most 1 vertex has
(outDegree - inDegree) = 1and at most 1 vertex has(inDegree - outDegree) = 1and all other vertices have equal in and out degrees
Finding an Eulerian Path - Time Complexity - O(E)
Code - Reconstruct Itinerary LC332